Fire Opal's QAOA Solver
An overview of Fire Opal's end-to-end managed tool for execution of QAOA algorithms
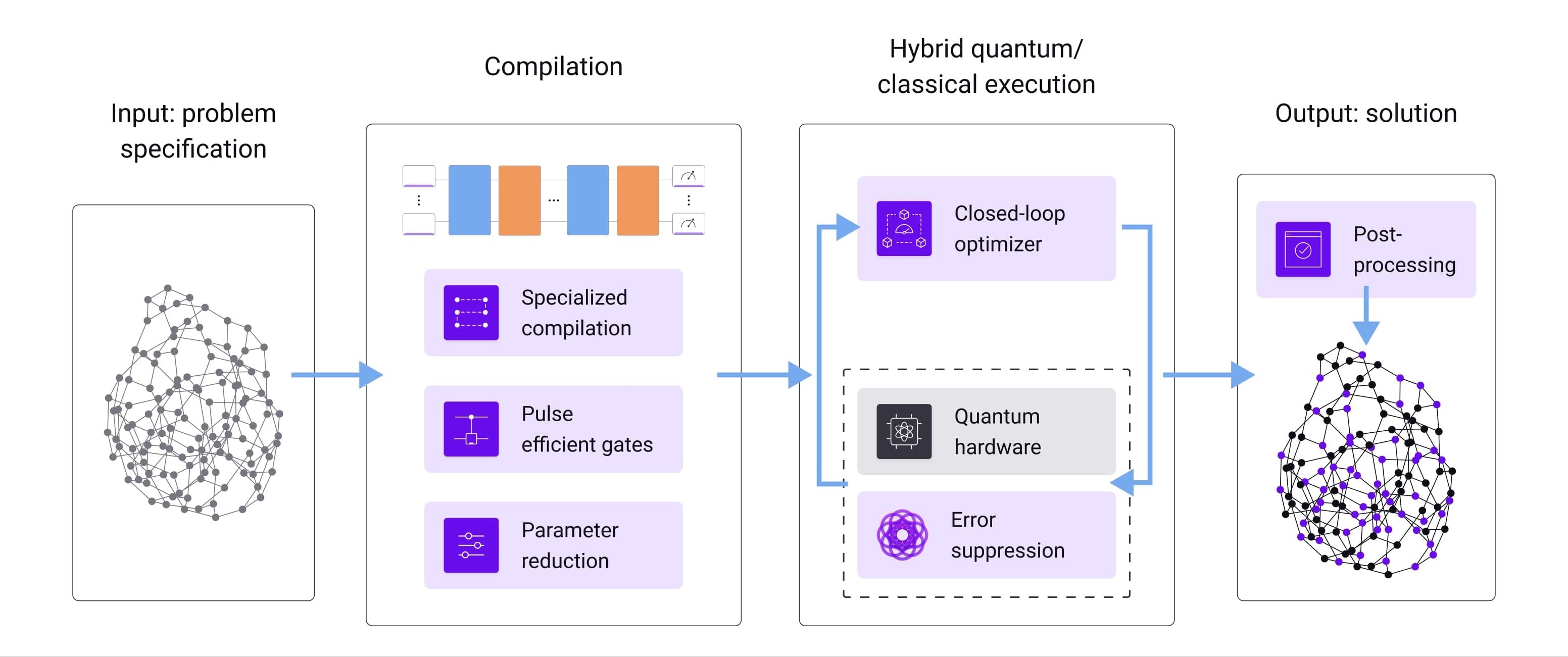
Fire Opal offers a single, easy-to-use function to run Quantum Approximate Optimization Algorithm (QAOA) algorithms. With this function, all aspects of execution are fully optimized and automated, from hardware-level error suppression to efficient problem mapping to closed-loop classical optimization.
To jump right in and see how the QAOA Solver is used, check out the application note on Solving Max-Cut using Fire Opal.
Intro to QAOA
QAOA is a popular algorithm that can be applied to a wide range of optimization problems that are out of reach today like portfolio optimization, efficient logistics routing, and asset liability management.
QAOA is part of a broader family of hybrid quantum-classical algorithms, Variational Quantum Algorithms (VQAs), which involve encoding the problem into a function with a set of parameters, where the goal is to find the values of the parameters that optimize the result of the function. VQAs leverage classical optimization techniques, such as machine learning, to optimize the parameters of quantum circuits, while using quantum computers to evaluate the parameters against the function.
Hybrid quantum-classical algorithms combine the processing power of both quantum and classical computers and leverage the benefits of each to solve problems more efficiently. Hybrid quantum-classical computing is essential to deriving value from quantum processors in the NISQ era, and it will remain relevant even in the age of fault-tolerant quantum computing, given that classical computers are likely to still be superior at handling certain workloads.
How Fire Opal solves typical implementation challenges
Implementing QAOA can be complex and typically requires a deep understanding of both quantum physics and optimization. Typically, setting up a QAOA problem and implementation requires several steps, such as:
- Defining the state-preparation circuit (also known as the ansatz)
- Defining the cost function
- Choosing initial parameters
- Implementing classical optimization techniques to optimize the parameters
- Repeatedly executing the circuit
Even when experts set up the problem correctly, most implementations of QAOA rarely ever converge or provide an answer better than random selection when executed on real hardware.
Fire Opal’s solve_qaoa function alleviates the complexity of running QAOA algorithms by providing a single function that performs the entire execution process and consistently returns the correct answer.
To invoke solve_qaoa, you can specify one of two input types:
- A graph, represented a NetworkX
Graph, and a problem type, such as"maxcut" - A cost function, represented as a SymPy
expr
Performance benefits
Fire Opal's QAOA Solver provides a greater probability of achieving the correct result on real hardware compared with most other implementations. This benefit is due to improvements of all aspects of the optimization routine, which are outlined below in the "Behind the scenes" section.
Benchmarking tests were performed comparing Fire Opal to an open source implementation of QAOA that is referred to as the default. In ten repeated trials of a MaxCut problem, Fire Opal converged on the correct solution every time, whereas the default never produced a correct answer.
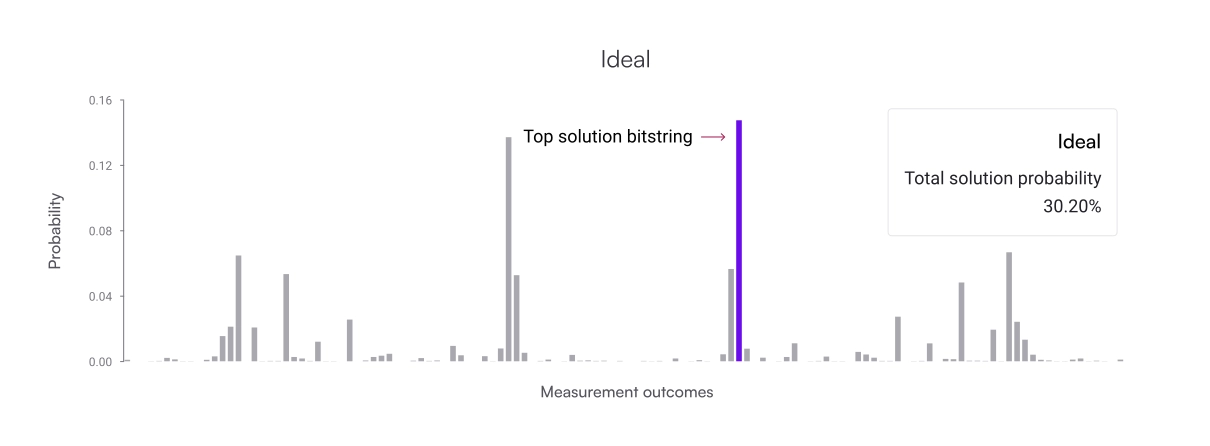
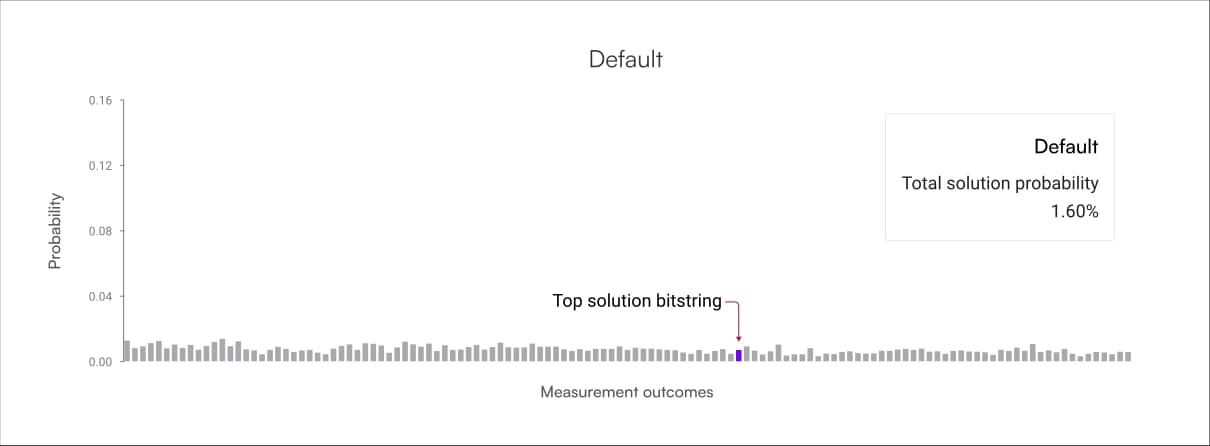
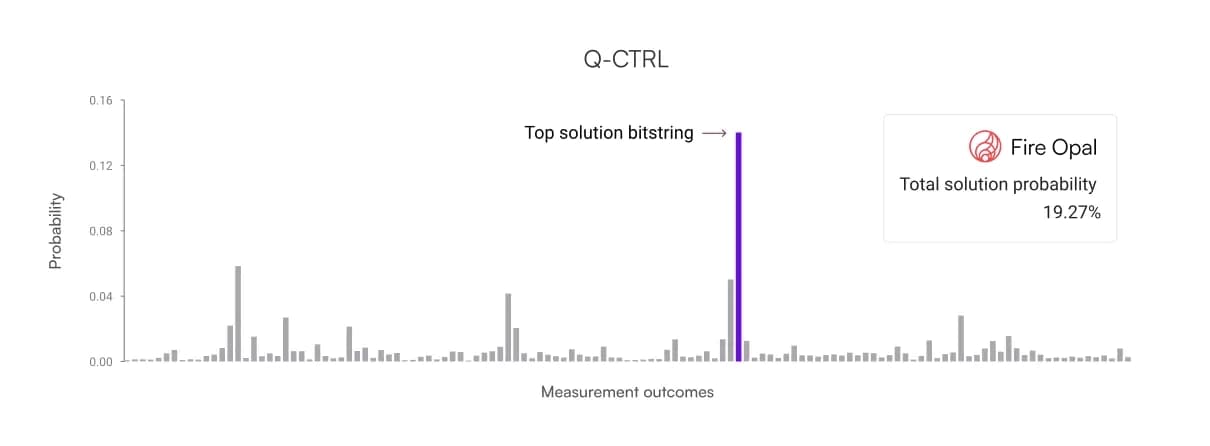
The histograms below show the results of one of these experiments. First shown is the ideal probability distribution generated by a noiseless simulator, followed by the default results and the Fire Opal results, respectively. The solution bitstring is highlighted in purple in all three graphs, and because there are multiple correct solutions to this problem, the ideal solution probability is only around thirty percent. On the default plot, the solution bitstring is indistinguishable from the other outcomes due to noise. Comparitively, this bitstring stands out as the highest probability answer on the Fire Opal results. Fire Opal improved the likelihood of obtaining the correct answer by 12×.
Because Fire Opal greatly improves the probability of achieving the correct answer on each iteration, the overall optimization loop is able to converge on the correct answer in fewer steps with a high degree of confidence. The graph below shows the number of optimization steps executed by the routine plotted against the solution probability.
Typically in QAOA implementation, the algorithm will converge and stop the iterative loop once a solution probability is reached beyond a certain threshold of probability. In the case of the default implementation, it was unable to converge on an answer even once within the ten trials performed, whereas Fire Opal converged on the correct solution within twenty steps each time.
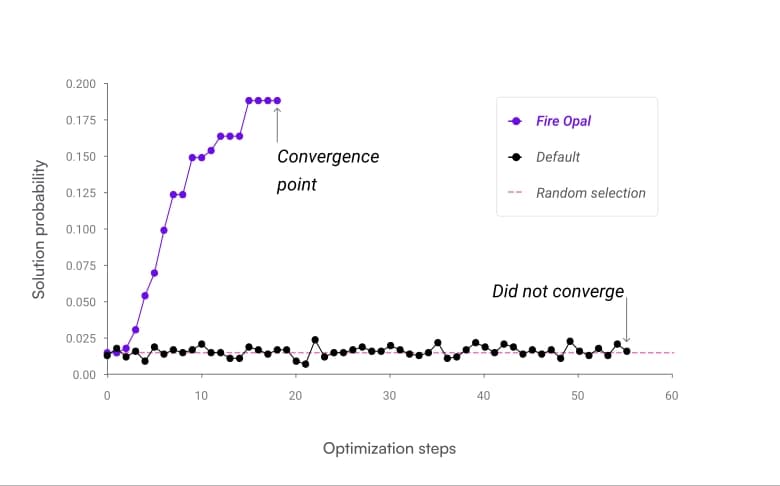
By significantly improving the chances of obtaining the correct answer and reducing the number of executions, Fire Opal can save a tremendous amount of time and resources.
Types of problems
Any type of QAOA problem can be solved using the solve_qaoa function, which covers a wide range of combinatorial optimization problems, such as Set Packing, Graph Partitioning, Job Sequencing, Traveling Salesman, and more. MaxCut is the first problem where you can simply specify your goal and the problem type—"maxcut"—as input parameters.
NOTE Most problems can be represented as a cost function with N-qubit terms. Fire Opal places no upper limit on N, meaning that polynomial cost functions of quadratic and higher order are supported. However, Fire Opal does not accept polynomial problems that are linear, as these problems are considered trivial. Although we can solve these trivial problems with quantum resources, we choose not to accept them for the following reasons:
- Being a user of quantum resources is expensive, and these problems can easily be solved by popular python libraries such as
numpy,scipy, orsympy. - We want to optimize usage of our resources to solve more rigorous problems.
- We want to avoid having 100% classical pathways in our QAOA solver.
Behind the scenes
Fire Opal's QAOA solver delivers best-in-class results on real hardware by combining several methods developed by Q-CTRL's expert team of quantum researchers. These methods include:
- Fire Opal’s error suppression pipeline: The QAOA solver leverages the best-in-class error suppression provided by the
executefunction, which improves the quality of individual circuit execution. - Specialized compilation: The input circuit is transformed by parallelizing multi-qubit gate operations to produce a more compact circuit and reduced duration.
- Pulse-efficient gates: On top of optimizing the implementation of the native gate set, Fire Opal identifies recurring complex gates and optimizes their direct implementation at the pulse-level. This technique cuts duration in half compared to standard decomposition.
- Parameter Reduction: A compact functional transformation is used to reduce the number of parameters to be optimized in the variational quantum algorithm. This reduces problem complexity and results in more efficient convergence.
- Bounding Parameters: The parameter landscape is constrained using properties, such as periodicity and symmetries of the problem, effectively reducing the resources needed for optimization.
- Aggregate Objective Function: Low cost bitstrings are prioritized instead of using a standard sample mean. This further improves the probability of obtaining optimal solution bitstrings at the convergence point.
- Closed-Loop Optimizer: Fire Opal's closed-loop optimizer converges efficiently and consistently in the presence of device noise.
Now that you've learned all about Fire Opal's QAOA Solver, try it out yourself by running the tutorial Solving MaxCut using Fire Opal.
