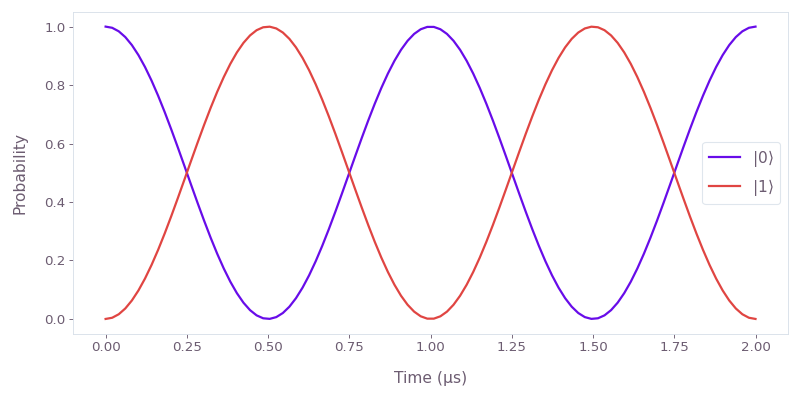
plot_population_dynamics
- qctrlvisualizer.plot_population_dynamics(sample_times, populations, *, figure=None)
Create a plot of the dynamics of the specified populations.
- Parameters:
sample_times (np.ndarray) – The 1D array of times in seconds at which the populations have been sampled.
populations (dict) – The dictionary of populations to plot, of the form
{"label_1": population_values_1, "label_2": population_values_2, ...}. Each population_values_n is a 1D array of population values with the same length as sample_times and label_n is its label. Population values must lie between 0 and 1.figure (matplotlib.figure.Figure or None, optional) – A matplotlib Figure in which to place the plots. If passed, its dimensions and axes will be overridden.
Examples
Plot the Rabi oscillations of a single qubit with initial state \(|0\rangle\) under the Hamiltonian \(H = \omega \sigma_x\).
import matplotlib.pyplot as plt import numpy as np import boulderopal as bo from qctrlvisualizer import plot_population_dynamics graph = bo.Graph() omega = 2 * np.pi * 0.5e6 # rad/s duration = 2e-6 # s hamiltonian = graph.constant_pwc_operator( duration, omega * graph.pauli_matrix("X") ) sample_times = np.linspace(0.0, duration, 100) unitaries = graph.time_evolution_operators_pwc( hamiltonian=hamiltonian, sample_times=sample_times, name="unitaries" ) initial_state = graph.fock_state(2, 0)[:, None] evolved_states = unitaries @ initial_state evolved_states.name = "states" result = bo.execute_graph(graph=graph, output_node_names=["states"]) states = result["output"]["states"]["value"] qubit_populations = np.abs(states.squeeze()) ** 2 plot_population_dynamics( sample_times=sample_times, populations={rf"$|{k}\rangle$": qubit_populations[:, k] for k in [0, 1]}, )